Sfdwhf

Orthographic projections
A₅Coxeter plane

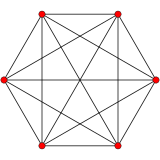5-simplex

In 5-dimensional geometry, there are 19 uniform polytopes with A₅ symmetry. There is one self-dual regular form, the 5-simplex with 6 vertices.

Each can be visualized as symmetric orthographic projections in Coxeter planes of the A₅ Coxeter group, and other subgroups.

Graphs

Symmetric orthographic projections of these 19 polytopes can be made in the A₅, A₄, A₃, A₂Coxeter planes. A_k graphs have [k+1] symmetry. For even k and symmetrically nodea_1ed-diagrams, symmetry doubles to [2(k+1)].

These 19 polytopes are each shown in these 4 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

#	Coxeter plane graphs				Coxeter-Dynkin diagram Schläfli symbol Name
	[6]	[5]	[4]	[3]
	A5	A4	A3	A2
1					{3,3,3,3} 5-simplex (hix)
2					t1{3,3,3,3} or r{3,3,3,3} Rectified 5-simplex (rix)
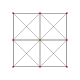
3					t2{3,3,3,3} or 2r{3,3,3,3} Birectified 5-simplex (dot)
4					t0,1{3,3,3,3} or t{3,3,3,3} Truncated 5-simplex (tix)
5					t1,2{3,3,3,3} or 2t{3,3,3,3} Bitruncated 5-simplex (bittix)
6					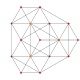t0,2{3,3,3,3} or rr{3,3,3,3} Cantellated 5-simplex (sarx)
7					t1,3{3,3,3,3} or 2rr{3,3,3,3} Bicantellated 5-simplex (sibrid)
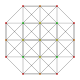
8					t0,3{3,3,3,3} Runcinated 5-simplex (spix)
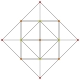
9					t0,4{3,3,3,3} or 2r2r{3,3,3,3} Stericated 5-simplex (scad)
10					t0,1,2{3,3,3,3} or tr{3,3,3,3} Cantitruncated 5-simplex (garx)
11					t1,2,3{3,3,3,3} or 2tr{3,3,3,3} Bicantitruncated 5-simplex (gibrid)
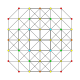
12					t0,1,3{3,3,3,3} Runcitruncated 5-simplex (pattix)
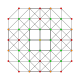
13					t0,2,3{3,3,3,3} Runcicantellated 5-simplex (pirx)
14					t0,1,4{3,3,3,3} Steritruncated 5-simplex (cappix)
15					t0,2,4{3,3,3,3} Stericantellated 5-simplex (card)
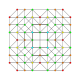
16					t0,1,2,3{3,3,3,3} Runcicantitruncated 5-simplex (gippix)
17					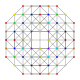t0,1,2,4{3,3,3,3} Stericantitruncated 5-simplex (cograx)
18					t0,1,3,4{3,3,3,3} Steriruncitruncated 5-simplex (captid)
19					t0,1,2,3,4{3,3,3,3} Omnitruncated 5-simplex (gocad)

A5 polytopes
t0	t1	t2	t0,1	t0,2	t1,2	t0,3
t1,3	t0,4	t0,1,2	t0,1,3	t0,2,3	t1,2,3	t0,1,4
t0,2,4	t0,1,2,3	t0,1,2,4	t0,1,3,4	t0,1,2,3,4

References

• 
  H.S.M. Coxeter:
  
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  
  


• 
  Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, .mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
  ISBN 978-0-471-01003-6 ^[1]
  
  
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  
  
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  
  
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
  
  
  
  


• 
  N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

• 
  Klitzing, Richard. "5D uniform polytopes (polytera)".
  

Notes